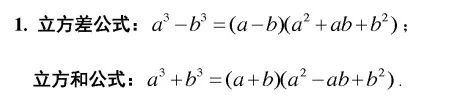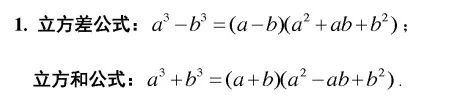无码一区二区三区爆白浆_久久精品无码一区二区三区_亚洲中文字幕无码AV_免费无码又爽又刺激高潮视频_日韩精品无码人成视频手机

高中數(shù)學(xué)50個常考的二級結(jié)論

瀏覽次數(shù)： 發(fā)布日期： 2024-12-17 18:10:20

5. 平行四邊形對角線平方之和等于四條邊平方之和.

12. 過橢圓準(zhǔn)線上一點作橢圓的兩條切線，兩切點連線所在直線必經(jīng)過橢圓相應(yīng)的焦點.

13. 圓錐曲線的切線方程求法：隱函數(shù)求導(dǎo).

推論：

14. 切點弦方程：平面內(nèi)一點引曲線的兩條切線，兩切點所在直線的方程叫做曲線的切點弦方程.

22. 過橢圓上一點做斜率互為相反數(shù)的兩條直線交橢圓于A、B兩點，則直線AB的斜率為定值.

24. 拋物線焦點弦的中點，在準(zhǔn)線上的射影與焦點F的連線垂直于該焦點弦.

25. 雙曲線焦點三角形的內(nèi)切圓圓心的橫坐標(biāo)為定值a(長半軸長).

26. 對任意圓錐曲線，過其上任意一點作兩直線，若兩直線斜率之積為定值，兩直線交曲線于A，B兩點，則直線AB恒過定點.

32. 角平分線定理：三角形一個角的平分線分其對邊所成的兩條線段與這個角的兩邊對應(yīng)成比例。

角平分線定理逆定理：如果三角形一邊上的某個點分這條邊所成的兩條線段與這條邊對角的兩邊對應(yīng)成比例，那么該點與對角頂點的連線是三角形的一條角平分線.

39. 帕斯卡定理：如果一個六邊形內(nèi)接于一條二次曲線(橢圓、雙曲線、拋物線)，那么它的三對對邊的交點在同一條直線上.

45. 三角形五心的一些性質(zhì)：

(1)三角形的重心與三頂點的連線所構(gòu)成的三個三角形面積相等；

(2)三角形的垂心與三頂點這四點中，任一點是其余三點所構(gòu)成的三角形的垂心；

(3)三角形的垂心是它垂足三角形的內(nèi)心；或者說，三角形的內(nèi)心是它旁心三角形的垂心；

(4)三角形的外心是它的中點三角形的垂心；

(5)三角形的重心也是它的中點三角形的重心；

(6)三角形的中點三角形的外心也是其垂足三角形的外心；

(7)三角形的任一頂點到垂心的距離，等于外心到對邊的距離的二倍.

編輯：陳婷婷

來源：高中生學(xué)習(xí)方法

聲明：以上圖文，貴在分享，版權(quán)歸原作者及原出處所有。如涉及版權(quán)等問題，請及時與我們聯(lián)系。